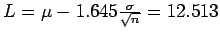Statistics 1060: Practice Solutions Week 8

5.5

$\begin{array}{\vert l\vert c\vert} \hline Exact \ Probability & 0.2312 \\ \hli... ... & 0.2061 \\ \hline Table \ Normal \ with \ CC & 0.2327 \\ \hline \end{array}$

a) There are 150 independent observations, each with probability of "success" p=0.5.

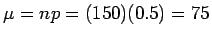b) $\mu = np = (150)(0.5) = 75$.

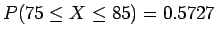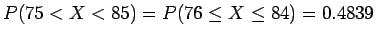c) The mean is (200)(0.4) = 80. We could interpret "between 75 and 85" as $P(75 \le X \le 85) = 0.5727$ (or see line 1 of table). Or we could exclude 75 or 85 and find $P(75 < X < 85) = P(76 \le X \le 84) = 0.4839$ (or see line 2 of table).

d) 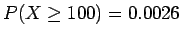$P(X \ge 100) = 0.0026$ (or see line 3 of table).


5.9

$\begin{array}{\vert l\vert c\vert c\vert c\vert} \hline Exact \ Probability & 0... ...ine Table \ Normal \ with \ CC & 0.7286 & 0.8714 & 0.9660\\ \hline \end{array}$

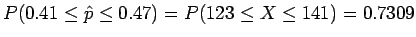a) Find $P(0.41 \le \hat{p} \le 0.47) = P(123 \le X \le 141) = 0.7309$ (table, line 1).

b) For 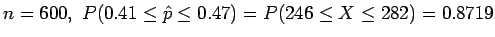$n = 600, \ P(0.41 \le \hat{p} \le 0.47) = P(246 \le X \le 282) = 0.8719$ (table, line 2).

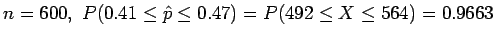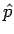For $n = 600, \ P(0.41 \le \hat{p} \le 0.47) = P(492 \le X \le 564) = 0.9663$ (table, line 3). Larger sample sizes are more likely to produce values of $\hat{p}$ close to the true value of p.


5.13

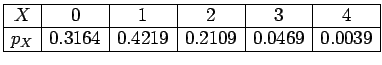
$\begin{array}{\vert c\vert c\vert c\vert c\vert c\vert c\vert} \hline X & 0 & 1... ...hline p_{X} & 0.3164 & 0.4219 & 0.2109 & 0.0469 & 0.0039 \\ \hline \end{array}$

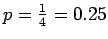a) n = 4 and $ p = \frac{1}{4} = 0.25$.

b) The distribution is below; the histogram is at the right.

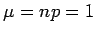
c) $\mu = np = 1$


5.19

$\begin{array}{\vert l\vert c\vert} \hline Normal \ Approximation & 0.2134\\ \h... ...al & 0.2148\\ \hline Table \ Normal \ with \ CC & 0.2266\\ \hline \end{array}$

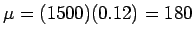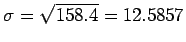a) $\mu = (1500)(0.12) = 180$ and $\sigma = \sqrt{158.4} = 12.5857$.

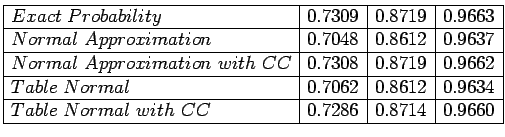
b) np = 180 and n(1 - p) = 1320 are both more than 10. Normal approximation values for 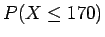$P(X \le 170)$ are in the table.


5.21

$\begin{array}{\vert l\vert c\vert c\vert} \hline Normal \ Approximation & 0.124... ...36\\ \hline Table \ Normal \ with \ CC & 0.1492 & 0.0401\\ \hline \end{array}$

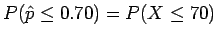a) $P(\hat{p} \le 0.70) = P(X \le 70)$ is in row 1.

b) 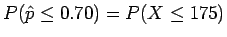$P(\hat{p} \le 0.70) = P(X \le 175)$ is in row 2.

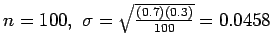
c) 400; With $n = 100, \ \sigma = \sqrt{\frac{(0.7)(0.3)}{100}} = 0.0458$

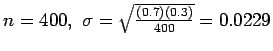
With $n = 400, \ \sigma = \sqrt{\frac{(0.7)(0.3)}{400}} = 0.0229$

d) Yes. Regardless of p, n must be quadrupled to cut the standard deviation in half.


5.29

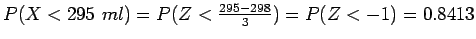
a) $P(X < 295 \ ml) = P(Z < \frac{295 - 298}{3}) = P(Z < -1) = 0.8413$

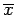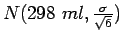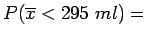
b) $\overline{x}$ has a $N(298 \ ml, \frac{\sigma}{\sqrt{6}})$ distribution, so $P(\overline{x} < 295 \ ml)=$

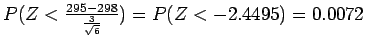$P(Z < \frac{295 - 298}{\frac{3}{\sqrt{6}}}) = P(Z < -2.4495) = 0.0072$ (table value: 0.0071)


5.33

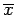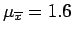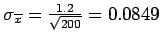$\overline{x}$ is approximately normal with $\mu_{\overline{x}} = 1.6$ and $\sigma_{\overline{x}} = \frac{1.2}{\sqrt{200}} = 0.0849$ flaws.

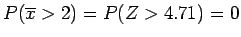$P(\overline{x} > 2) = P(Z > 4.71) = 0$ (essentially).


5.35

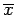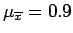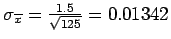a) $\overline{x}$ is approximately normal with $\mu_{\overline{x}} = 0.9$ and $\sigma_{\overline{x}} = \frac{1.5}{\sqrt{125}} = 0.01342$ g/mi.
b) P(Z > 2.326) = 0.01 if Z is N(0,1), so L = 0.9 + (2.326)(0.01342) = 0.9312 g/mi

5.37

$L = \mu - 1.645\frac{\sigma}{\sqrt{n}} = 12.513$


STATISTICS 1060 HOMEPAGE PREVIOUS PAGE
Jonathan Payne
1999-03-12