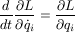 ,
,
U = U(q0,q1,...,qn-1)for the potential energy, and an expression
T = T(q0,q1,...,qn-1,q'0,q'1,...,q'n-1)for the kinetic energy of the system in terms of these coordinates. From this data, Lagrangian Mechanics allows us to predict the behavior of the system. The behavior is expressed as a system of n second-order differential equations. The Lagrangian equations of motion are
where L = T - U. Equivalently,,
Here we assume that L has no explicit time dependency, i.e. that the variable t does not occur in the formula for L. There is one equation for each coordinate i. The above is a system of linear equations Aq''+Bq'=v, where.
for i,j=0..n-1. At any given time in the evolution of the system, qj and q'j are known. The Lagrange Applet uses a numerical method to solve the above equations for q''i and to display the solution graphically.,
The Lagrange Applet defines an abstract Java class MechSystem that can numerically solve these equations and display the motion of a system. For each particular type of mechanical system, one defines a subclass of MechSystem. This subclass must essentially define two things: methods for calculating the potential and kinetic energy, and methods for how the system is to be drawn. In addition, some methods must be defined for bookkeeping: for instance, methods that return the names and number of coordinates and constants. One can also define methods for handling mouse action, but this is optional.
Back to main Lagrange page.
Back to Peter Selinger's Homepage:
![]()