Statistics 1060: Practice Solutions Week 10

6.23

No. The interval refers to the mean math score, not to individual scores, which will be much more variable (indeed, if more than 95% of students score below 470, they are not doing very well).


6.27

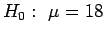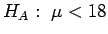a) $H_{0}: \ \mu = 18$ sec; $H_{A}: \ \mu < 18$ sec.

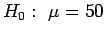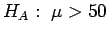b) $H_{0}: \ \mu = 50$; $H_{A}: \ \mu > 50$.

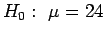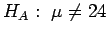c) $H_{0}: \ \mu = 24$; $H_{A}: \ \mu \neq 24$.


6.29

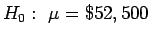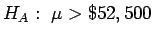a) $H_{0}: \ \mu = \$52, 500$; $H_{A}: \ \mu > \$52, 500$.

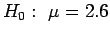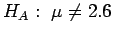b) $H_{0}: \ \mu = 2.6$ hr; $H_{A}: \ \mu \neq 2.6$ hr.


6.33

There almost certainly was some difference between the sexes and between blacks and whites; the observed difference between men and woman was so large that it is unlikely to be due to chance. For black and white students, however, the difference was small enough that it could be attributed to random variation.


6.35

a) 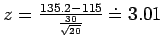$z = \frac{135.2 - 115}{\frac{30}{\sqrt{20}}} \doteq 3.01$, which gives P = 0.0013. We reject H0 and conclude that the older students do have a higher mean score.

b) We assume the 20 students were an SRS, and that the population is (nearly) normal - near enough that the distribution of 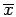$\overline{x}$ is close to normal. The assumption that we have an SRS is important.


6.37

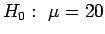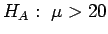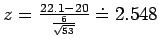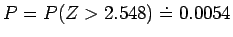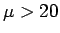a) $H_{0}: \ \mu = 20$; $H_{A}: \ \mu > 20$. $z = \frac{22.1 - 20}{\frac{6}{\sqrt{53}}} \doteq 2.548$, so $P = P(Z > 2.548) \doteq 0.0054$. This is strong evidence that $\mu > 20$ - the students have a higher average than past students have.

b) Randomly assign some (25-30) students to take the course, and compare their ACT mean score with those who did not take the course.


6.45

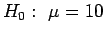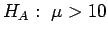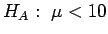Since 0.215 < 0.674, P > 0.25. (In fact, P = P(Z > 0.215) = 0.4149). This assumes that the test gave some (weak) evidence in favour of the alternative, e.g., we had $H_{0}: \ \mu = 10$ vs. $H_{A}: \ \mu > 10$. If the alternative had been $H_{A}: \ \mu < 10$, then P = P(Z < 0.215), which is even bigger - that is, it gives even less reason to reject H0.


6.55

a) 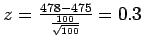$z = \frac{478 - 475}{\frac{100}{\sqrt{100}}} = 0.3$, so P = P(Z > 0.3) = 0.3821.

b) 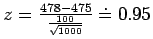$z = \frac{478 - 475}{\frac{100}{\sqrt{1000}}} \doteq 0.95$, so P = P(Z > 0.95) = 0.1711.

c) 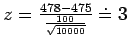$z = \frac{478 - 475}{\frac{100}{\sqrt{10000}}} \doteq 3$, so P = P(Z > 3) = 0.0013.


STATISTICS 1060 HOMEPAGE PREVIOUS PAGE

Jonathan Payne
1999-03-10