- a)
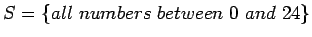
- b)

- c)
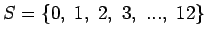
- d)
S = {all real numbers greater than or equal to zero} or
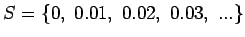
- e)
S = {all positive and negative numbers} (The rats can gain or lose weight)
- a)
The probability of type AB blood is
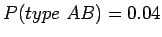 .
This is because the sum of each
probability in the distribution adds is 1. So in this case
1 - (0.49 + 0.27 + 0.20) = 0.04
.
This is because the sum of each
probability in the distribution adds is 1. So in this case
1 - (0.49 + 0.27 + 0.20) = 0.04
- b)
For a safe blood transfusion Maria needs either type O or B.

- a)
As the chart says, the percent of sons with lower-class fathers who reach the highest class is 0.01 or
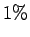 .
.
- b)
To be a discrete probability distribution, all probabilities in the distribution must be between
0 and 1 and all probabilities must add up to 1. As we can see all, probabilities are between 0 and 1 and their sum is
0.48 + 0.38 + 0.08 + 0.05 + 0.01 = 1 - c)
 .
.
- d)
Note that in c) the question asked for
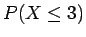 .
This probability include P(3). In this case we want all probabilities up to 3.
.
This probability include P(3). In this case we want all probabilities up to 3.
P(X < 3) = P(1) + P(2) = 0.86. - e)
P(son of lower-class father reaches one of two highest classes) =
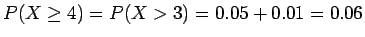 .
.
- a)
The percent of 5th graders that finished grade 12 is 0.752 or
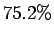 .
.
- b)
All probabilities are between 0 and 1 and their sum is 1.
- c)
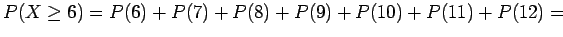
0.007 + 0.013 + 0.032 + 0.068 + 0.070 + 0.041 + 0.752 = 0.983 - d)
P(X > 6) = 0.013 + 0.032 + 0.068 + 0.070 + 0.041 + 0.752 = 0.976
- e)
P(completed at least 1 year of high school) =

- a)
Let A, B and C be students 1, 2, and 3 respectively. P(student opposes) = 0.40, so P(student supports) = 0.60.
Since each student's opinion is independent from each other, the probability that A and B support and C opposes is
P(A supports and B supports and C opposes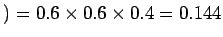
- b)
All the possible combinations of opinions that can be held by students A, B, and C are SSS, SSO, SOS, SOO, OSS, OSO, OOS, OOO
where S = support and O = oppose.

P(SSO) = P(SOS) = P(OSS) = 0.144
P(SOO) = P(OSO) = P(OOS) = 0.096
P(OOO) = 0.064
- c)
Let X be the number of students who oppose.
P(X = 0) = P(SSS) = 0.216

P(X = 2) = 0.288
P(X = 3) = 0.064
- d)
This is either
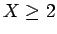 or X > 1.
or X > 1.
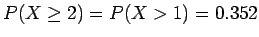
We know
![]() so the mean grade in the course is:
so the mean grade in the course is:
0(0.10) + 1(0.15) + 2(0.30) + 3(0.30) + 4(0.15) = 2.25
- a)
X and Y would seem to be independent. Rainfall a year apart should not be related.
- b)
X and Y would be dependent (or not independent) here. Weather patterns can last for several days.
- c)
Again dependent. The two locations are close together and weather patterns stretch over great distances.
- a)
The probability that a woman chosen is 65 years old or older is the number of woman who are 65 years or older divided by the total
number of woman:

- b)
We know the woman is 65 years old or older so the probability that she is married is the number of 65 year old woman or older who
are married divided by the total number of woman 65 years old or older:
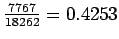
- c)
There are 7,767 woman in the 65 years old and older age group who are married.
P(over 65 and married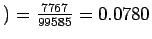
- d)
P( over 65 and married) = P( married | over 65) =
(0.1834)(0.4253) = 0.0780
- a)
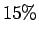 of adults drink only cola.
of adults drink only cola.
- b)
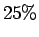 of adults drink neither of the three.
of adults drink neither of the three.
Let F ={dollar falls} and R ={renegotiation demand}
![]()
Let:
F ={dollar falls}
RF ={renegotiation demand if dollar falls}
N ={dollar does not fall}
RN ={renegotiation demand if dollar does not fall}
![]() =
=
![]()
The probability Linda gives the correct answer to a question is
![]()
0.75 + (0.25)(0.2) = 0.80